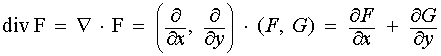What else can I help you with?
What is physical significance of divergence?
Divergence is a vector operator that measures the magnitude of a vector fields source or sink at a given point.
Examples of divergence of a vector field?
I am not sure if this is the answer you are looking for, since the question is listed in both Physics and Abstract Algebra, so I will try to give you some examples from physics. One of the indicators of a divergence of a vector field is the presence of a source. For example the electric field can be represented by a vector field, with each vector pointing along the field and has a length proportional to the strength of the electric field at that position. A point source then causes an electric field with a divergence at the location of the point source, with the vectors all pointing away from it (positive charge) or towards it (negative charge). Another example would be some point mass and the Newtonian gravitational field. One of Maxwell's equations states that the magnetic field cannot have any divergences meaning that there are no magnetic monopoles.
How does vector calculus apply in fluid mechanics?
The velocity at each point in the fluid is a vector. If the fluid is compressible, the divergence of the velocity vector is nonzero in general. In a vortex the curl is nonzero.
Is magnetic field line scalar or vector quantity?
Vector.
The direction of the electric field vector is defined as?
Direction of the electric field vector is the direction of the force experienced by a charged particle in an external electric field.
What is the physical meaning of divergence?
Divergence is a measure of how a vector field spreads out or converges at a given point in space. It indicates whether the flow of a vector field is expanding or contracting at that point.
What is an example of the divergence of a tensor in the context of mathematical analysis?
An example of the divergence of a tensor in mathematical analysis is the calculation of the divergence of a vector field in three-dimensional space using the dot product of the gradient operator and the vector field. This operation measures how much the vector field spreads out or converges at a given point in space.
What is the physical interpretation of divergence in the context of vector fields?
In the context of vector fields, divergence represents the rate at which the field's vectors are spreading out from or converging towards a point. It indicates how much the field is expanding or contracting at that point.
What is the physical meaning of divergence in the context of vector fields?
In the context of vector fields, divergence represents the rate at which the field's vectors are spreading out from or converging towards a point. It indicates how much the field is expanding or contracting at that point.
What is transformed divergence?
Transformed divergence is a concept in vector calculus that involves calculating the divergence of a vector field after applying a transformation to the coordinate system. This technique is often used to simplify calculations in complex systems by changing the coordinate system to make the divergence easier to compute.
What is physical significance of divergence?
Divergence is a vector operator that measures the magnitude of a vector fields source or sink at a given point.
Examples of divergence of a vector field?
I am not sure if this is the answer you are looking for, since the question is listed in both Physics and Abstract Algebra, so I will try to give you some examples from physics. One of the indicators of a divergence of a vector field is the presence of a source. For example the electric field can be represented by a vector field, with each vector pointing along the field and has a length proportional to the strength of the electric field at that position. A point source then causes an electric field with a divergence at the location of the point source, with the vectors all pointing away from it (positive charge) or towards it (negative charge). Another example would be some point mass and the Newtonian gravitational field. One of Maxwell's equations states that the magnetic field cannot have any divergences meaning that there are no magnetic monopoles.
What is the significance of the divergence of a scalar times a vector in the context of vector calculus?
The significance of the divergence of a scalar times a vector in vector calculus is that it simplifies to the scalar multiplied by the divergence of the vector. This property is important in understanding how scalar fields interact with vector fields and helps in analyzing the flow and behavior of physical quantities in various fields of science and engineering.
Continuity equation for time varying field?
The continuity equation for a time-varying field relates the divergence of the field with the rate of change of field strength at any given point. Mathematically, it is expressed as ∇⋅E = -∂ρ/∂t, where ∇ is the divergence operator, E is the field, ρ is the charge density, and ∂/∂t represents the partial derivative with respect to time. This equation ensures that the field and charge distributions are consistent over time, in accordance with the principle of charge conservation.
What is the difference between curl and divergence?
Divergence: rate of spread of vector in free space for non closed path. and Curl: rate of spread of vector in free space for closed path.
Is the Laplacian a vector?
No, the Laplacian is not a vector. It is a scalar operator used in mathematics and physics to describe the divergence of a gradient.
How does vector calculus apply in fluid mechanics?
The velocity at each point in the fluid is a vector. If the fluid is compressible, the divergence of the velocity vector is nonzero in general. In a vortex the curl is nonzero.