0
What else can I help you with?
What is this expression as the cosine of an angle cos30cos55 plus sin30sin55?
cos(30)cos(55)+sin(30)sin(55)=cos(30-55) = cos(-25)=cos(25) Note: cos(a)=cos(-a) for any angle 'a'. cos(a)cos(b)+sin(a)sin(b)=cos(a-b) for any 'a' and 'b'.
Prove that secB - cosB equals tanBsinB?
Try to write everything in terms of sines and cosines:1 / cos B - cos B = (sin B / cos B) sin B1 / cos B - cos B = sin2B / cos BMultiply by the common denominator, cos B:1 - cos2B = sin2BUse the pithagorean identity on the left side:sin2B + cos2B - cos2B = sin2Bsin2B = sin2B
What are five trigonometric identities?
All others can be derived from these and a little calculus: sin2x+cos2x=1 sec2x-tan2x=1 sin(a+b)=sin(a)cos(b)+sin(b)sin(a) cos(a+b)=cos(a)cos(b)-sin(a)sin(b) eix=cos(x)+i*sin(x)
How do you proof the formula sin2A equals 2sinAcosA?
First, note that sin(a+b)=sin(a)cos(b)+sin(b)cos(a)[For a proof, see: www.mathsroom.co.uk/downloads/Compound_Angle_Proof.pptFor the case of b=a, we have:sin (a+a)=sin(a)cos(a)+sin(a)cos(a)sin (2a)=2*sin(a)cos(a)
Use trigonometric identities to write each expression in terms of a single trigonometric function or a constant. simplify cos t sin t?
Thanks to the pre-existing addition and subtraction theorums, we can establish the identity:sin(a+b) = sin(a)cos(b)+sin(a)cos(b)Then, solving this, we getsin(a+b) = 2(sin(a)cos(b))sin(a)cos(b) = sin(a+b)/2a=b, sosin(a)cos(a) = sin(a+a)/2sin(a)cos(a) = sin(2a)/2Therefore, the answer is sin(2a)/2.
How do I find the product z1z2 if z1 5(cos20 plus isin20) and z2 8(cos15 plus isin15)?
Like normal expansion of brackets, along with: cos(A + B) = cos A cos B - sin A sin B sin(A + B) = sin A cos B + cos A sin B 5(cos 20 + i sin 20) × 8(cos 15 + i sin 15) = 5×8 × (cos 20 + i sin 20)(cos 15 + i sin 15) = 40(cos 20 cos 15 + i sin 15 cos 20 + i cos 15 sin 20 + i² sin 20 sin 15) = 40(cos 20 cos 15 - sin 20 cos 15 + i(sin 15 cos 20 + cos 15 sin 20)) = 40(cos(20 +15) + i sin(15 + 20)) = 40(cos 35 + i sin 35)
How would you prove left cosA plus sinA right times left cos2A plus sin2A right equals cosA plus sin3A?
You need to make use of the formulae for sin(A+B) and cos(A+B), and that cos is an even function: sin(A+B) = cos A sin B + sin A cos B cos(A+B) = cos A cos B - sin A sin B cos even fn → cos(-x) = cos(x) To prove: (cos A + sin A)(cos 2A + sin 2A) = cos A + sin 3A The steps are to work with the left hand side, expand the brackets, collect [useful] terms together, apply A+B formula above (backwards) and apply even nature of cos function: (cos A + sin A)(cos 2A + sin 2A) = cos A cos 2A + cos A sin 2A + sin A cos 2A + sin A sin 2A = (cos A cos 2A + sin A sin 2A) + (cos A sin 2A + sin A cos 2A) = cos(A - 2A) + sin(A + 2A) = cos(-A) + sin 3A = cos A + sin 3A which is the right hand side as required.
Express cos4x sin3x in a series of sines of multiples of x?
The best way to answer this question is with the angle addition formulas. Sin(a + b) = sin(a)cos(b) + cos(a)sin(b) and cos(a + b) = cos(a)cos(b) - sin(a)sin(b). If you compute this repeatedly until you get sin(3x)cos(4x) = 3sin(x) - 28sin^3(x) + 56sin^5(x) - 32sin^7(x).
If a cos theta plus b sin theta equals 8 and a sin theta - b cos theta equals 5 show that a squared plus b squared equals 89?
Well, darling, if we square the first equation and the second equation, add them together, and do some algebraic magic, we can indeed show that a squared plus b squared equals 89. It's like a little math puzzle, but trust me, the answer is as sassy as I am.
What is the exact value of the expression cos 7pi over 12 cos pi over 6 -sin 7pi over 12 sin pi over 6?
cos(a)cos(b)-sin(a)sin(b)=cos(a+b) a=7pi/12 and b=pi/6 a+b = 7pi/12 + pi/6 = 7pi/12 + 2pi/12 = 9pi/12 We want to find cos(9pi/12) cos(9pi/12) = cos(3pi/4) cos(3pi/4)= cos(pi-pi/4) cos(pi)cos(pi/4)-sin(pi)sin(pi/4) cos(pi)=-1 sin(pi)=0 cos(pi/4) = √2/2 sin(pi/4) =√2/2 cos(pi)cos(pi/4)-sin(pi)sin(pi/4) = - cos(pi/4) = -√2/2
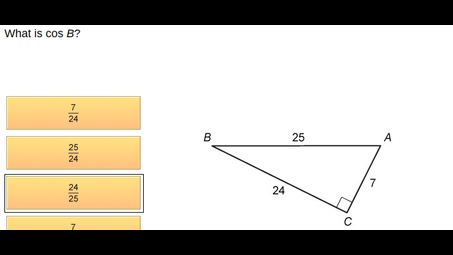
What is the cos of angle B?
.385
Find angle B in triangle ABC if a is 10 b 16 and c 12?
We can use the law of cosines here. ( remember, side b is opposite angle B) DEGREE MODE! b^2 = a^2 + c^2 - 2ac cos(B) 16^2 = 10^2 + 12^2 - 2(10)(12) cos(B) 256 = 244 - 240(cos B ) 12 = -240(cos B ) -0.05 = cosB arcos(-0.05) = B B = 93 degrees
