0
What else can I help you with?
Is LMN OPQ If so name the congruence postulate that applies?
congruent - SSSAnswer by Arteom, Friday December 10, 2010
What are necessary when proving that the diagonals of a rectangle are congruent?
A ruler or a compass would help or aternatively use Pythagoras' theorem to prove that the diagonals are of equal lengths
Complete this sentence after a congruence transformation the area of a triangle would be it was before?
This sentence can be complete as: After a congruence transformation the area of a triangle would be the same as it was before.
A statement that is accepted as true without proof Also called an axion?
That would be a postulate
What else would need to be congruent to show that efg is congruent to hij by sss?
Ah, what a lovely question! To show that triangles EFG and HIJ are congruent by Side-Side-Side (SSS), we would need to ensure that all three pairs of corresponding sides are equal in length. Additionally, the corresponding angles would also need to be congruent to fully demonstrate the congruence between the two triangles. Just remember to take your time, be gentle with yourself, and enjoy the process of exploring geometry.
What theorem is used to prove the AAS triangle congruence theorem?
Excuse me, but two triangles that have A-A-S of one equal respectively to A-A-S of the other are not necessarily congruent. I would love to see that proof!
What other information do you need in order to prove the triangles congruent using the SAS Congruence Postulate?
To prove triangles congruent using the SAS (Side-Angle-Side) Congruence Postulate, you need to know the lengths of two sides of one triangle and the included angle between those sides, as well as the corresponding lengths of the two sides and the included angle of the other triangle. Specifically, you would need to confirm that the two pairs of sides are equal in length and that the angle between those sides in both triangles is congruent. With this information, you can establish the congruence of the triangles.
What is ass or ssa congruence postulate?
The ASS postulate would be that:if an angle and two sides of one triangle are congruent to the corresponding angle and two sides of a second triangle, then the two triangles are congruent.The SSA postulate would be similar.Neither is true.
IF you are using this figure to prove the isosceles triangle theorem would be the best strategy?
To prove the Isosceles Triangle Theorem using a figure, the best strategy is to focus on the properties of the triangle's angles and sides. Start by labeling the two equal sides and their opposite angles. Then, use triangle congruence criteria, such as the Side-Angle-Side (SAS) or Angle-Side-Angle (ASA), to establish that the two triangles formed by drawing a line from the vertex to the base are congruent. This congruence will demonstrate that the base angles are equal, thereby proving the theorem.
Is ABC DEF name the congruence postulate that applies?
The "ABC DEF" naming convention does not directly refer to a specific congruence postulate in geometry. However, congruence postulates generally include Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Side-Angle (ASA) among others. To determine which postulate applies, you would need to specify the relationships between the angles and sides of triangles ABC and DEF.
Which postulate or theorem can be used to prove that triangle PRS is congruent to triangle QRS?
We cannot determine without seeing the data for PRS & QRS. My guess though would be ASA Though it could also be SSS
What is difference in axiom and postulate?
Theorem: A Proven Statement. Postulate: An Accepted Statement without Proof. They mean similar things. A postulate is an unproven statement that is considered to be true; however a theorem is simply a statement that may be true or false, but only considered to be true if it has been proven.
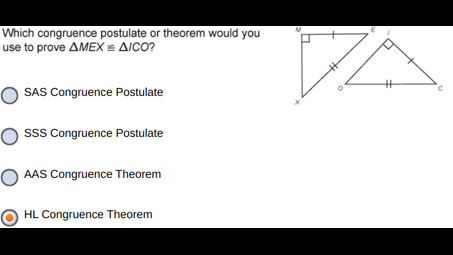
What postulate or theorem would you use to prove the triangles are congruent?
To prove that two triangles are congruent, you can use the Side-Angle-Side (SAS) Postulate. This states that if two sides of one triangle are equal to two sides of another triangle, and the angle between those sides is also equal, then the triangles are congruent. Alternatively, the Angle-Side-Angle (ASA) Theorem can also be used if two angles and the included side of one triangle are equal to the corresponding parts of another triangle.
which statement completes the paragraph proof?
I'm happy to help! Please provide the paragraph or the statement you would like me to complete.
The AA Similarity Postulate states that two triangles are similar if they have?
You would use the AA Similarity Postulate to prove that the following two triangles are similar. True or false?
Is LMN OPQ If so name the congruence postulate that applies?
congruent - SSSAnswer by Arteom, Friday December 10, 2010
Did Pythagoras prove his own Theorem?
Yes, he must have proved his own Theorem otherwise it would not have been adopted by mathematicians across the globe. I'm sure you could test out the theorem: check whether c2 really does equal b2 + a2 in a manual measurement of a triangle; though this is less accurate and not as precise as the Theorem.
