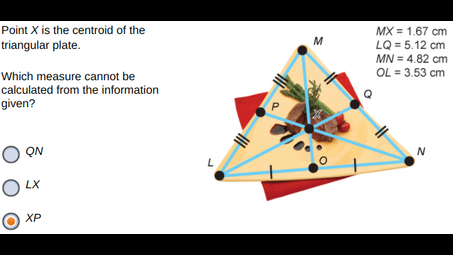
what- Point X is the centroid of the triangular plate.Which measure cannot be calculated from the information given?
What else can I help you with?
Is it true the centroid of a triangle is the center of gravity for a triangular region?
Yes.
What is the formula for the centroid of a n-dimensional hypersphere?
The centroid is the centre. How you find it depends on what information you have about the hypersphere.
Where is the centroid of a triangle used in real life?
The centroid of a triangle, which is the point where the three medians intersect, is used in various real-life applications, such as engineering and architecture for structural stability analysis. It helps in determining the center of mass for triangular shapes, which is crucial in designing safe and efficient structures. Additionally, in computer graphics, the centroid aids in modeling and rendering shapes, ensuring accurate simulations and animations. In navigation and robotics, the centroid can assist in path planning and obstacle avoidance by representing optimal positions within triangular formations.
Where should string be attached to triangular-shaped pieces of cardboard so they will balance in a mobile?
To balance triangular-shaped pieces of cardboard in a mobile, attach the string to the centroid (the center of mass) of each triangle. The centroid can be found by connecting the midpoints of each side to the opposite vertex, forming smaller triangles. By suspending each piece from its centroid, it will hang evenly and maintain balance when in motion. Ensure that the strings are of equal length for uniformity in the mobile.
What are medians and what is the point called where they meet?
The median of a triangle is a straight line from a vertex to the midpoint of the opposite side. The three medians of a triangle meet at the centroid. If the triangle is made of uniform material the centroid is the centre of mass of the triangular shape.
Is it true that the centroid of a triangle is the center of gravity for a triangular region?
True
Is it true the centroid of a triangle is the center of gravity for a triangular region?
Yes.
The center of gravity of a triangular solid with uniform thicknees and density is?
centroid
What is another name for the centroid of a triangular solid with uniform thickness and density?
center of gravity
Another name for the centroid of a triangular solid with uniform thickness and density is the?
center of gravity
Where does the center of gravity of a triangular lamina lie?
The center of gravity of a triangular lamina lies at the point of intersection of the medians of the triangle, which is also known as the centroid. It is located one-third of the distance from each vertex to the midpoint of the opposite side along the median.
What is the center of gravity of a triangular solid with uniform thickness and density is?
the centroid the point at which one can balance the triangle
What is the formula for the centroid of a n-dimensional hypersphere?
The centroid is the centre. How you find it depends on what information you have about the hypersphere.
The centroid of a triangular solid with uniform thickness and density is the?
the point shared by a triangle's medians the point at which one can balance the triangle
Where is the centroid of a triangle used in real life?
The centroid of a triangle, which is the point where the three medians intersect, is used in various real-life applications, such as engineering and architecture for structural stability analysis. It helps in determining the center of mass for triangular shapes, which is crucial in designing safe and efficient structures. Additionally, in computer graphics, the centroid aids in modeling and rendering shapes, ensuring accurate simulations and animations. In navigation and robotics, the centroid can assist in path planning and obstacle avoidance by representing optimal positions within triangular formations.
Where should string be attached to triangular-shaped pieces of cardboard so they will balance in a mobile?
To balance triangular-shaped pieces of cardboard in a mobile, attach the string to the centroid (the center of mass) of each triangle. The centroid can be found by connecting the midpoints of each side to the opposite vertex, forming smaller triangles. By suspending each piece from its centroid, it will hang evenly and maintain balance when in motion. Ensure that the strings are of equal length for uniformity in the mobile.
What are medians and what is the point called where they meet?
The median of a triangle is a straight line from a vertex to the midpoint of the opposite side. The three medians of a triangle meet at the centroid. If the triangle is made of uniform material the centroid is the centre of mass of the triangular shape.