What else can I help you with?
Abc is a right angled triangle ac equals 6cm bc equals 9cm work out the length of ab give your answer to 3 sig figures?
If angle ACB is the right angle then ab is the hypotenuse. Then, (ab)2 = 62 + 92 = 36 + 81 = 117 ab = √117 = 10.8 (3 sf) If angle BAC is the right angle then ab is one leg of a right angled triangle with bc the hypotenuse. 92 = 62 + (ab)2 : (ab)2 = 92 - 62 = 81 - 36 = 45 ab = √45 = 6.71 (3 sf)
What is the length of ad if the hypotenuse of the right angles are ab 20 bc 15 and abd and abc?
If the sides of the triangle are 20 and 15 then by using Pythagoras' theorem the length of the hypotenuse works out as 25 units of measurement.
In the given right triangle find the length of the hypotenuse AB if BC 6 and AC 5.?
The length is sqrt(61) units.
If AB equals 0 what is the angle between a and b?
Zero.For instance, given a right triangle with points ABC. where AC is the hypotenuse, then to find the angle between AB, we take sin(AB/AC), where AB is the distance between points A and B, and AC is the distance between A and C. If we replace AB with 0, the equation would be sin(0/AC). Sine of zero is always zero.
Triangle ABC is a right triangle. If side AC is 7 units and side BC is 10 units what is the measure of side AB?
By using Pythagoras' theorem for a right angle triangle if side AB is the hypotenuse it is the square root of 149 which is about 12.207 rounded to three decimal places
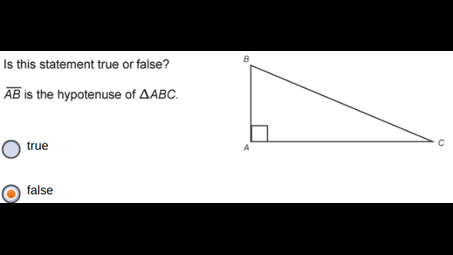
is this statement true or false If you fold the paper so that A matches up with B and then creases the paper, the line formed by the crease is the perpendicular bisector of AB.?
true
What Is the Statement of Pythagoras theorem?
Pythagoras ' theorem states that in a right angled triangle ABCAB2+BC2 = AC2, where AB and BC are the perpendicular sides of the triangle and AC is the hypotenuse(the longest side).
What is the length of the hypotenuse of the rigth triangle ABC in if AC 6 and AD 5?
Assuming you mean side AB is 5: If angle B is the right angle, side AC is the hypotenuse and is of length 6. If angle A is the right angle, side BC is the hypotenuse and is of length sqrt(52 + 62) ~= 7.81 Angle C cannot be the right angle as then side AB would be the hypotenuse but the hypotenuse is the longest side and side AB is shorter than AC.
What is the length of the hypotenuse AC?
sqrt(ab^2 + bc^2)
Triangle abc is a right triangle if side ac equals 5 and side bc equals 6 what is the measure of side ab?
If CB is the hypotenuse, then AB measures, √ (62 - 52) = √ 11 = 3.3166 (4dp) If AB is the hypotenuse then it measures, √ (62 + 52) = √ 61 = 7.8102 (4dp)
Abc is a right angled triangle ac equals 6cm bc equals 9cm work out the length of ab give your answer to 3 sig figures?
If angle ACB is the right angle then ab is the hypotenuse. Then, (ab)2 = 62 + 92 = 36 + 81 = 117 ab = √117 = 10.8 (3 sf) If angle BAC is the right angle then ab is one leg of a right angled triangle with bc the hypotenuse. 92 = 62 + (ab)2 : (ab)2 = 92 - 62 = 81 - 36 = 45 ab = √45 = 6.71 (3 sf)
Segment ab equals 9 segment bc equals 12 what is the hypotenuse of right triangle abc?
15
Haydn's keyboard sonata in Ab major?
This is a statement, not question.
What is the length of ad if the hypotenuse of the right angles are ab 20 bc 15 and abd and abc?
If the sides of the triangle are 20 and 15 then by using Pythagoras' theorem the length of the hypotenuse works out as 25 units of measurement.
How do you prove ab equals ba?
A - B = B - AThis statement is very difficult to prove.Mainly because it's not true . . . unless 'A' happens to equal 'B'.
If AB does not equal 3x then AB 3x or AB 3x?
If AB does not equal 3x, then AB must either be less than 3x or greater than 3x. This means we can express the relationship as AB < 3x or AB > 3x. The statement highlights that AB cannot be equal to 3x by definition.
In the given right triangle find the length of the hypotenuse AB if BC 6 and AC 5.?
The length is sqrt(61) units.