when you multiply a function by -1 what is the effect on its graph?
Lilly Fritts
Multiplying a function by -1 will make it a reflection of the original function across the x axis.
John Climer
Jonathan Block
The function will remain unchanged. Therefore, the graph will also remain unchanged.
Add your answer:
Graph of an inverse proportion is an?
The graph of the function y(x) = 1/x is a hyperbola.
What is y equals 3x?
I don't understand your question but y=3x is the function of a graph, to graph the function you would plug points into the function such as x=0, x=1, x=-1 and you would find the y values at each point so that you can graph it. In this case the graph is a parabola which has a u shape.
What happen to the graph of a function when you multiply the function rule by a?
If a > 0, it is stretched, in the vertical direction, by the factor a If a = 1 it is unchanged If 0 < a < 1, it is shrunk bt the factor a If a = 0, it is coincident with the x-axis If a < 0 then as above, but it is also reflected about the x-axis (turned upside down).
How can you graph a linear function without a calculator?
y=x+1
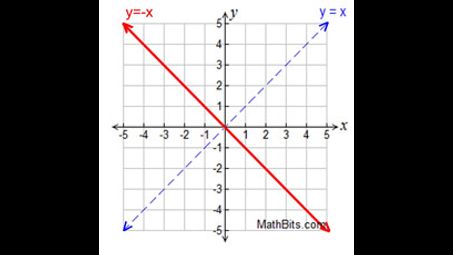
What is the linear parent function?
The linear parent function is y=x. The line on a graph passes through the origin(0,0) with a slope of 1. The line will face left to right on the graph like this /.
What is the effect on a graph when you multiply a function by -1?
When a function is multiplied by -1 its graph is reflected in the x-axis.
Which operation flips the graph of a function over the x-axis?
Multiply by -1
If the parents function is y4x which is the function of the graph?
The function y = x is the graph that passes from the points (-1, -1), (0, 0), and (1, 1) The function y = 4x is the graph that passes form the points (-1, -4), (0, 0), and (1, 4) Sketch these graphs in a same x and y coordinate system, and you can see both of them
Graph of an inverse proportion is an?
The graph of the function y(x) = 1/x is a hyperbola.
Explain how the graph of fx ln x be used to graph the function gx ex -1?
graph gx is the reflection of graph fx and then transformed 1 unit down
What is y equals 3x?
I don't understand your question but y=3x is the function of a graph, to graph the function you would plug points into the function such as x=0, x=1, x=-1 and you would find the y values at each point so that you can graph it. In this case the graph is a parabola which has a u shape.
What happen to the graph of a function when you multiply the function rule by a?
If a > 0, it is stretched, in the vertical direction, by the factor a If a = 1 it is unchanged If 0 < a < 1, it is shrunk bt the factor a If a = 0, it is coincident with the x-axis If a < 0 then as above, but it is also reflected about the x-axis (turned upside down).
How can you graph a linear function without a calculator?
y=x+1
What is the area bounded by the graph of the function fx equals 1 - e to the power of -x over the interval -1 2?
What is the area bounded by the graph of the function f(x)=1-e^-x over the interval [-1, 2]?
What line test is used to determine if a graph is a 1-1 function?
2
How does the graph of the cosine function differ from a graph of a sine function?
the graph of cos(x)=1 when x=0the graph of sin(x)=0 when x=0.But that only tells part of the story. The two graphs are out of sync by pi/2 radians (or 90°; also referred to as 1/4 wavelength or 1/4 cycle). One cycle is 2*pi radians (the distance for the graph to get back where it started and repeat itself.The cosine graph is 'ahead' (leads) of the sine graph by 1/4 cycle. Or you can say that the sine graph lags the cosine graph by 1/4 cycle.
What is function if X is -1 and y is 4?
It is impossible to determine the function here. (-1,4) is just a point on a graph.
