0
What else can I help you with?
How many different types of semiregular tessellations are there?
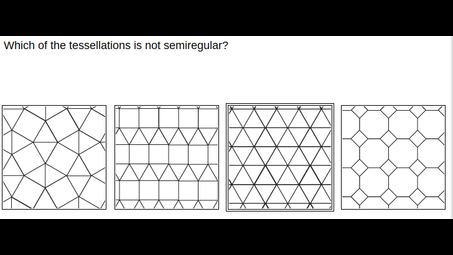
There are eight different types of semiregular tessellations. Also called Archimedean tessellations, they occur when two or more convex regular polygons form tessellations of the plane in a way each polygon vertex is surrounded by the same polygons and in the same order.
Are Uniform tessellations are semiregular?
By the use of wording "uniform" you are in fact stating that the tesselations are "regular"
What does a dot sign mean in a problem?
A dot in a problem can mean multiply. For example: 7.8=56 It also can mean the arrangement of angles about each vertex point. (Look up semiregular tessellations) It is typed like this: 3.3.4.3.4
Must all the edges of a semiregular polyhedron be the same length?
must all edges of semiregular polyhedron be the same length
How are tessellations related to math?
Its trigonometry. Tessellations are shapes.
Who discovered tessellations?
Johannes Kepler discovered and studied tessellations.
What are shapes that fit together with no gaps called?
Shapes that fit perfectly together are called a tessellation.
What occupations use tessellations in their work?
Artists, designers, architects, and mathematicians are some occupations that use tessellations in their work. For artists and designers, tessellations can be used in creating patterns and designs. In architecture, tessellations can be utilized in developing tiling and paving designs. Mathematicians study the properties and characteristics of tessellations as part of geometry.
Did Marjorie Rice invented tessellations?
Marjorie Rice didn't invent tessellations, which have been around for a long time - but she did discover at least 4 previously unknown tessellations.
How many semi-regular tessellations are there?
there are 8 possible semi-regular tessellations :) hop i can helpp .
What polygons can be used to make tessellations?
Regular tessellations can be made using triangles, squares, and hexagons.
Tessellations that use more than one type of regular polygon are called regular tessellations.?
Actually, tessellations that use more than one type of regular polygon are called semi-regular or Archimedean tessellations, not regular tessellations. Regular tessellations consist of only one type of regular polygon repeating in a pattern. Examples of regular tessellations include those formed by equilateral triangles, squares, or hexagons. Semi-regular tessellations combine two or more different types of regular polygons while still covering a plane without gaps or overlaps.
