What else can I help you with?
How many medians are needed to find the centroid of a triangle?
Two. However, you can actually do it with just one. Consider the median AD of triangle ABC. Then the point G, 2/3 of the way from A to D, is the centroid. This process (2/3 of the way from the vertex to the opposite side) can be applied to any median.
If the median to a side of a triangle is also an altitude to that side then the triangle is isosceles How do you write this Proof?
Let the triangle be ABC and suppose the median AD is also an altitude.AD is a median, therefore BD = CDAD is an altitude, therefore angle ADB = angle ADC = 90 degreesThen, in triangles ABD and ACD,AD is common,angle ADB = angle ADCand BD = CDTherefore the two triangles are congruent (SAS).And therefore AB = AC, that is, the triangle is isosceles.
Can triangle abc be a right triangle if side ac2 side bc3 and side ab4?
No.
What is the median formula?
It depends on whether you mean median in terms of statistical data or the line joining a vertex of a triangle to the midpoint of the opposite side. The Statistical Median: If there are n observations where n is odd, then the median is the (n+1)/2 smallest observation. If n is even, then the median is the arithmetical mean of the n/2 and n/2+1 smallest observations. The Coordinate Geometry Median: Given triangle ABC, with A = (xa, ya), B = (xb, yb) and C = (xc, yc), the midpoint, D of BC is [(xb+xc)/2, (yb+yc)/2] and so, the equation of the median AD is (y-ya)/(x-xa) = (2ya-yb-yc)/(2xa-xb-xc)
What side of ABC is the longest?
Any side: you can select the order in which the vertices are named!
If bd is both the altitude and median of abc then abc is?
Isosceles
If is both the altitude and median of triangle ABC then triangle ABC is .?
It is isosceles.
If is both the altitude and median of triangle ABC then triangle ABC is?
It is isosceles.
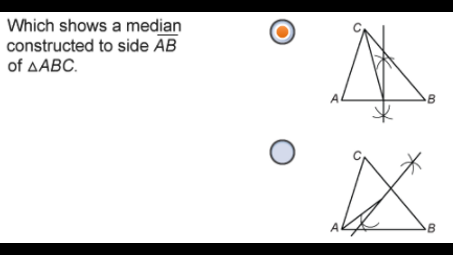
In ABC point D is the midpoint of AC. Which term describes BD?
It is a median.
Is ABC family still on basic cable?
ABC Family is on basic cable and has many shows that are good for families. Shows on ABC Family can also be watched online.
Why is abc making you sign in to watch shows?
ABC has people sign into watch shows so they can see how many people are watching their shows via online.
Where can one watch ABC episodes?
One cannot watch the ABC channel for free online, but some of their shows can be watched for free on their official website. It is only available to residents of the USA.
What is the formula to calculate the length of median of a triangle?
m^2=(2b^2+2c^2-a^2)/4 where m is the median of triangle ABC.
Are there any TV shows like Supernanny aired on ABC?
Yes, Supernanny is on Abc!!!!
How many medians are needed to find the centroid of a triangle?
Two. However, you can actually do it with just one. Consider the median AD of triangle ABC. Then the point G, 2/3 of the way from A to D, is the centroid. This process (2/3 of the way from the vertex to the opposite side) can be applied to any median.
Is switched at birth the best abc family show in the world?
ABC family shows over 50 shows but switched at birth is like an angel to my ears!
If the median to a side of a triangle is also an altitude to that side then the triangle is isosceles How do you write this Proof?
Let the triangle be ABC and suppose the median AD is also an altitude.AD is a median, therefore BD = CDAD is an altitude, therefore angle ADB = angle ADC = 90 degreesThen, in triangles ABD and ACD,AD is common,angle ADB = angle ADCand BD = CDTherefore the two triangles are congruent (SAS).And therefore AB = AC, that is, the triangle is isosceles.