What else can I help you with?
What are five trigonometric identities?
All others can be derived from these and a little calculus: sin2x+cos2x=1 sec2x-tan2x=1 sin(a+b)=sin(a)cos(b)+sin(b)sin(a) cos(a+b)=cos(a)cos(b)-sin(a)sin(b) eix=cos(x)+i*sin(x)
Can you use the law of sines if 3 sides are given?
Yes, but you would need to know a degree measure too. [Sin(A)/a] = [Sin(B)/b] = [Sin(C)/c] [a/Sin(A)] = [b/Sin(B)] = [c/Sin(C)]
How do you derived the sine law?
Consider any triangle ABC, and let AD be the altitude from A on to BC. Then sin(B) = AD/AB so that AD = AB*sin(B) and sin(C) = AD/AC so that AD = AC*sin(C) Therefore AB*sin(B) = AC*sin(C) or c*sin(B) = b*sin(C) where the lower case letter represents the side opposite the angle with the upper case name. Divide both sides by bc to give sin(B)/b = sin(C)/c. Similarly, using the altitude from B you can show that sin(A)/a = sin(C)/c. Combining with the previous result, sin(A)/a = sin(B)/b = sin(C)/c.
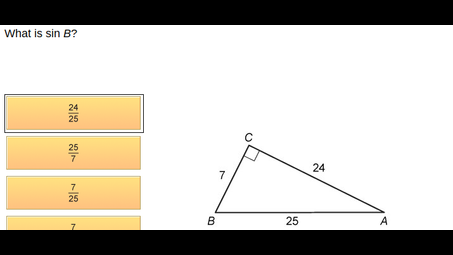
When abc are angles of a triangle prove sin2a sin2b sin2c4sinasinbsinc?
To prove that ( \sin^2 a \sin^2 b \sin^2 c = 4 \sin a \sin b \sin c ) for angles ( a, b, c ) of a triangle, we can use the identity ( a + b + c = 180^\circ ). The sine of angle ( c ) can be expressed as ( \sin c = \sin(180^\circ - (a + b)) = \sin(a + b) = \sin a \cos b + \cos a \sin b ). By substituting and manipulating these identities, we can derive the relationship, confirming the equality holds for the angles of a triangle.
How do you proof the formula sin2A equals 2sinAcosA?
First, note that sin(a+b)=sin(a)cos(b)+sin(b)cos(a)[For a proof, see: www.mathsroom.co.uk/downloads/Compound_Angle_Proof.pptFor the case of b=a, we have:sin (a+a)=sin(a)cos(a)+sin(a)cos(a)sin (2a)=2*sin(a)cos(a)
How do you get the sides of the triangle when 3 angles are given and its perimeter?
You need to use the sine rule. If the three angles are A, B and C and the sides opposite them are named a, b and c then, by the sine rule, a/sin(A) = b/sin(b) = c/sin(C) Therefore b = a*sin(B)/sin(A) = a*y where y = sin(B)/sin(A) can be calculated and c = a*sin(C)/sin(A) = a*z where z = sin(C)/sin(A) can be calculated. then perimeter = p = a + b + c = a + ay + az = a*(1 + y + z) therefore a = p/(1 + y + z) or a = p/[1 + sin(B)/sin(A) + sin(C)/sin(A)]. Everything on the right hand side is known and so a can be calculated. Once that has been done, b = a*y and c = a*z.
Use trigonometric identities to write each expression in terms of a single trigonometric function or a constant. simplify cos t sin t?
Thanks to the pre-existing addition and subtraction theorums, we can establish the identity:sin(a+b) = sin(a)cos(b)+sin(a)cos(b)Then, solving this, we getsin(a+b) = 2(sin(a)cos(b))sin(a)cos(b) = sin(a+b)/2a=b, sosin(a)cos(a) = sin(a+a)/2sin(a)cos(a) = sin(2a)/2Therefore, the answer is sin(2a)/2.
What is the perimeter of a triangle when an angle of 57 degrees is opposite to a side of 14.5 inches and has another angle of 71 degrees?
The sum of tthe angles of a triangle is 180° which means the third angle is 180° - (57° + 71°) = 52° The sine rule gives: a/sin A = b/sin B = c / sin C where side a is opposites angle A, etc. The sine rule can be used to find the lengths of the other two sides when the angles are all known and one side length is known. Let angle A = 57°, then side a = 14.5 in. Let angle B = 71° and angle C = 52° Using the sine rule: a/sin A = b/ sin B → b = a × sin B/sin A Similarly, c = a × sin C/sin A → The perimeter = a + b + c = a + a × sin B/sin A + a × sin C/sin A = a(1 + sin B/sin A + sin C/sin A) = 14.5 in × (1 + sin 71° / sin 57° + sin 52° / sin 57°) ≈ 44.47 in ≈ 44.5 in
In a triangle ABC b equals 15 cm and c equals 25 cm and also angle B equals 32'15'Find the side a and other angles?
By the sine rule, sin(C)/c = sin(B)/b so sin(C) = 25/15*sin(32d15m) = 0.8894 so C = 62.8 deg or 117.2 deg. Therefore, A = 180 - (B+C) = 85.0 deg or 30.5 deg and then, using the sine rule again, a/sin(A) = b/sin(B) so a = sin(A)*b/sin(B) = 28 or a = 14.3
How do you find the length of third side when 2 sides and all three angles are known?
The Law of Sines: with triangle ABC, the angles are A, B, & C. The sides {a, b, & c} are opposite of the respective capital letter vertex.a/sin(A) = b/sin(B) = c/sin(C). You know the angles A, B, C; and two sides (say a & b).So side c = a*sin(C)/sin(A) = b*sin(C)/sin(B).You could also use the Law of Cosines: c^2 = a^2 + b^2 - 2*a*b*cos(C)
Express cos4x sin3x in a series of sines of multiples of x?
The best way to answer this question is with the angle addition formulas. Sin(a + b) = sin(a)cos(b) + cos(a)sin(b) and cos(a + b) = cos(a)cos(b) - sin(a)sin(b). If you compute this repeatedly until you get sin(3x)cos(4x) = 3sin(x) - 28sin^3(x) + 56sin^5(x) - 32sin^7(x).
How do you construct a triangle with perimeter 150 mm and a base angle 75 degrees and 30 degrees?
Perhaps you can ask the angel to shed some divine light on the question! Suppose the base is BC, with angle B = 75 degrees angle C = 30 degrees then that angle A = 180 - (75+30) = 75 degrees. Suppose the side opposite angle A is of length a mm, the side opposite angle B is b mm and the side opposite angle C is c mm. Then by the sine rule a/sin(A) = b/(sin(B) = c/sin(C) This gives b = a*sin(B)/sin(A) and c = a*sin(C)/sin(A) Therefore, perimeter = 150 mm = a+b+c = a/sin(A) + a*sin(B)/sin(A) + a*sin(C)/sin(A) so 150 = a*{1/sin(A) + sin(B)/sin(A) + sin(C)/sin(A)} or 150 = a{x} where every term for x is known. This equation can be solved for a. So draw the base of length a. At one end, draw an angle of 75 degrees, at the other one of 30 degrees and that is it!