What else can I help you with?
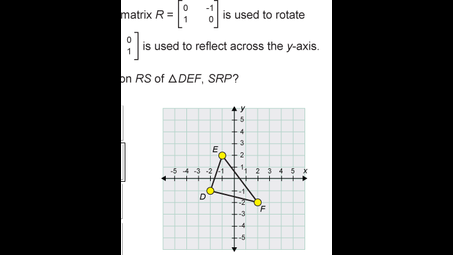
DEF with coordinates?
y=2x
DEF has coordinates?
-1, 2, -2 -2, -1, 2
How do you convert polar to rectangular coordinates?
If the polar coordinates of a point P are (r,a) then the rectangular coordinates of P are x = rcos(a) and y = rsin(a).
A point P has coordinates (3 2). What are its new coordinates after reflecting point P over the x-axis?
4875893948
How do you find the coordinates of a quadrilateral after reflecting it over the y axis?
If the coordinates of a point, before reflection, were (p, q) then after reflection, they will be (-p, q).
What are the possible coordinates of the midpoint of the given segment for AT?
The possible coordinates of the midpoint depend on the coordinates of A and T and these depend on what these two points are and how they are related.If A = (p,q) and T = (r,s ) then the midpoint of AT has coordinates [(p+r)/2, ((q+s)/2].
How do you rotate a shape 315 degrees clockwise about the origin?
The point with coordinates (p, q) will be rotated to the point with coordinates [(p - q)/sqrt(2), (p + q)/sqrt(2)].
A point P has coordinates (1, 4). What are its new coordinates after reflecting point P across the x-axis?
The answer is simple, it is: (-1, -4) EZ(Easy)
ABC has coordinates P?
2 down 1 up
What are the coordinates of points p and Q?
The 2-dimensional coordinates of p are (xp, yp) and those of Q are (xQ, yQ). I am not sure how that might help, but with the information provided that is the best that can be done.
What is the cardiod in mathematics?
In polar coordinates, p = 1 - sin(theta)
What are the coordinates of the color Carmine M and P?
215, 0, 64.