What else can I help you with?
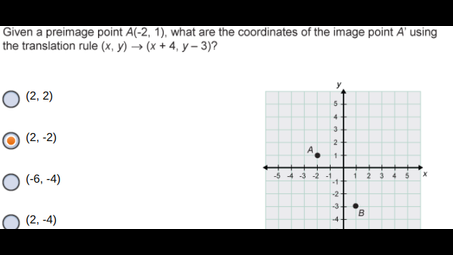
what- given a preimage point B (1, -3)?
4
What does pre image mean in math?
In mathematics, a preimage refers to the original set of elements that map to a particular element or set under a given function. Specifically, if ( f: X \to Y ) is a function and ( y \in Y ), the preimage of ( y ) (denoted as ( f^{-1}(y) )) is the set of all ( x \in X ) such that ( f(x) = y ). In the context of sets, the preimage of a subset ( B \subseteq Y ) is the set of all elements in ( X ) that map to ( B ) under the function ( f ).
How do you simplify 5-a-1 plus c-6a2 plus a2?
5 - a - 1 + c - 6a2 + a2
Solve x equals cx equals AA plus 1?
x = cx = aa+1 If x = cx, then c = 1 aa = a2 if a2 + 1 = x, then a2 = x-1 short of parametrization, this is the answer for this equation, but if you doing advanced maths, then let x= t (teR) a2 = -1 +t (teR)
What is the measure of angle 1 and angle 2 if angle 1 and angle 2 are complementary and angle 1 is 4 times greater than angle 2?
A1 + A2 = 90 A1 = 4*A2 Substituting from the second equation into the first: 4*A2 + A2 = 90 or 5*A2 = 90 so that A2 = 18 and then, by the second equations, A1 = 4*18 = 72
what- given a preimage point B (1, -3)?
4
How do you factorize 1-4y2?
1 - 4y2 can be expressed as 12 - (2y)2 which is of the form a2 - b2.Using the identity a2 - b2 = (a+b)(a-b) we can factorize the given algebraic expression as (1+2y)(1-2y).
How do you factor polynomial a4 plus a2?
( a2 ) ( a2+1 )
For each integer a if a2-1 is even then 4 divides a2-1?
Assuming it's a2-1 you mean. If a2-1 is even, it can be expressed as a2-1 = 2 * t, where t is a natural number. a2-1 = (a - 1)(a + 1) = 2 * t You immediately see that at least one of the terms in parenthesis has to be even, and then, that actually both have to be even, because (a + 1) - (a - 1) = 2. Therefore, you can express both of the terms as: a - 1 = 2 * s a + 1 = 2 *r, which gives us: 2 * s * 2 * r = a2 - 1, simplify: 4 * r * s = a2 - 1. Therefore, if a2-1 is even, a2-1 is also divisible by 4.
What does pre image mean in math?
In mathematics, a preimage refers to the original set of elements that map to a particular element or set under a given function. Specifically, if ( f: X \to Y ) is a function and ( y \in Y ), the preimage of ( y ) (denoted as ( f^{-1}(y) )) is the set of all ( x \in X ) such that ( f(x) = y ). In the context of sets, the preimage of a subset ( B \subseteq Y ) is the set of all elements in ( X ) that map to ( B ) under the function ( f ).
What is a squared plus a plus a aquared?
(a2 + a + a2) = (2a2 + a) = a (2a + 1)
How do you simplify 5-a-1 plus c-6a2 plus a2?
5 - a - 1 + c - 6a2 + a2
What should be subtracted from a2 -4a2 plus 5a2-6 to obatain a2-2a plus 1?
If I've read your question correctly, you need to subtract: a2 +2a -7 a2 -4a2 +5a2 -6 = 2a2 -6 Note, if x - y = z, then y = x - z; so: 2a2 -6 - (a2 -2a +1) = 2a2 -6 - a2 +2a -1 = a2 +2a -7
What is the answer for 3 over a plus 2 over a to the second power minus 1 over a to the third power?
a≠ 0,LCD = a33/a + 2/a2 - 1/a3= (3/a)(a2/a2) + (2/a2)(a/a) - 1/a3= 3a2/a3 + 2a/a3- 1/a3= (3a2 + 2a -1)/a3
What is the reciprocal of a plus bi if a2 plus b2 equals 1?
The reciprocal of a + bi is a - bi:1/(a + bi) since the conjugate is a - bi:= 1(a - bi)/[(a + bi)(a - bi)]= (a - bi)/[a2 - (b2)(i2)] since i2 equals to -1:= (a - bi)/(a2 + b2) since a2 + b2 = 1:= a - bi/1= a - bi
Solve x equals cx equals AA plus 1?
x = cx = aa+1 If x = cx, then c = 1 aa = a2 if a2 + 1 = x, then a2 = x-1 short of parametrization, this is the answer for this equation, but if you doing advanced maths, then let x= t (teR) a2 = -1 +t (teR)
What is the measure of angle 1 and angle 2 if angle 1 and angle 2 are complementary and angle 1 is 4 times greater than angle 2?
A1 + A2 = 90 A1 = 4*A2 Substituting from the second equation into the first: 4*A2 + A2 = 90 or 5*A2 = 90 so that A2 = 18 and then, by the second equations, A1 = 4*18 = 72