0
What else can I help you with?
Where is the shortest distance between any two points on the globe?
It depends on how complicated you want to make it. The generally accepted answer would be to start at one point, and make a line to the next (a straight line). That's gonna be the answer, say, your teacher might want (sorry if you're an adult :p). The technical answer? Drill a hole through the globe from one point to the other, and your shortest distance would be the straight line. Einstein's answer? A geodesic. Look it up :p
What is the point slope equation if the slope is 2?
If (p, q) is any point on the line, then the point slope equation is: (y - q)/(x - p) = 2 or (y - q) = 2*(x - p)
What is the point-slope formula and how is it used?
Given a straight line with slope m and a point (p,q) on the line, the point-slope formula of the line is (y - q) = m(x - p) It is used to represent a straight line in the Cartesian plane. This allows techniques of algebra to be used in solving problems in geometry.
How do you prove that a finite set of points cannot have any accumulation points in a complex analysis?
Complex analysis is a metric space so neighborhoods can be described as open balls. Proof follows a. Assume that the set has an accumulation point call it P. b. An accumulation point is defined as a point in which every neighborhood (open ball) around P contains a point in the set other than P. c. Since P is an accumulation point, I can choose an open ball around P that has a diameter less than the minimum distance between P and all elements of the finite set. Therefore there exists a neighbor hood around P which contains only P. Therefore P is not an accumulation point.
Show that of all line segments drawn from a given point not on it the perpendicular line segment is the shortest?
To show that the perpendicular line segment is the shortest among all line segments drawn from a given point not on it, we can use the Pythagorean theorem. Let the given point be P and the line segment be AB, with the perpendicular from P meeting AB at C. By the Pythagorean theorem, the sum of the squares of the two sides of a right triangle is equal to the square of the hypotenuse. In this case, PC is the hypotenuse, and AP and AC are the other two sides. Thus, AC (perpendicular line segment) will always be shorter than any other line segment AB drawn from point P.
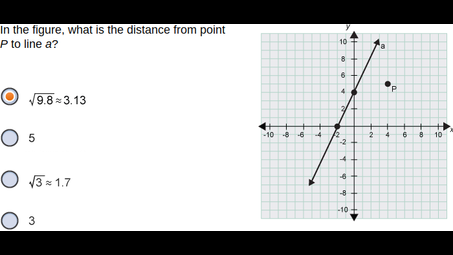
In the figure, what is the distance from point P to line a?
3v/ 2 ~ 4.2
what- in the figure, what is the distance from point P o line a?
3v/ 2 ~ 4.2
If Point p is on line m then how many plane are perpendicular to line m and also passes through point p?
1
What does area and perimeter mean?
P = the distance around a figure. A = the surface it takes up.
Where is the shortest distance between any two points on the globe?
It depends on how complicated you want to make it. The generally accepted answer would be to start at one point, and make a line to the next (a straight line). That's gonna be the answer, say, your teacher might want (sorry if you're an adult :p). The technical answer? Drill a hole through the globe from one point to the other, and your shortest distance would be the straight line. Einstein's answer? A geodesic. Look it up :p
is this statement true or falseThe steps for constructing a line perpendicular to a given line through point P are the same whether P lies on the line or not.?
false
What is point slope form of an equation of a line?
Given a point P = (a,b) and slope m, the equation of a line through P with slope m is (y-b) = m(x-a)
how to negate the hyperbolic parallel postulate?
The hyperbolic parallel postulate states that given a line L and a point P, not on the line, there are at least two distinct lines through P that do not intersect L.The negation is that given a line L and a point P, not on the line, there is at most one line through P that does not intersect L.The negation includes the case where there is exactly one such line - which is the Euclidean space.
is this statement true of false if point P is not on line L, the rhombus method can be used to construct a line M that is parallel to line L through P.?
true
What is the point slope equation if the slope is 2?
If (p, q) is any point on the line, then the point slope equation is: (y - q)/(x - p) = 2 or (y - q) = 2*(x - p)
What is the point-slope formula and how is it used?
Given a straight line with slope m and a point (p,q) on the line, the point-slope formula of the line is (y - q) = m(x - p) It is used to represent a straight line in the Cartesian plane. This allows techniques of algebra to be used in solving problems in geometry.
what- A highway on a map can be approximated by the line y = x + 1, where x and y are in tens of miles. Which of these is the distance from a house at point P(4, -3) to the highway?
4v/ 2~5.7
